The method
Monte Carlo method - also known as Monte Carlo simulation or Monte Carlo experiments - is a mathematical technique which allows someone to predict possible outcomes of an uncertain event. By definition, uncertainty and randomness are core aspects to this approach, and therefore Monte Carlo incorporates probabilities and random sampling to perform statistical analysis and generate numerical results.
In general, Monte Carlo simulations involve many unknown variables, which in turn increase the simulation model complexity, processing time and can make output interpretation challenging. The algorithm takes the variable(s) and assigns a random value to it (them) drawn from a selection of probability distributions. This process is repeated many times, and each time the algorithm assigns a new random value to the variable(s). In this way, the simulation is running a huge number of scenarios automatically, with many different values. Once the simulation is complete, the results are aggregated to provide estimates or other numeric values.
This technique is applied to a variety of domains such as
In principle Monte Carlo can be used to solve any problem that can have a probabilistic interpretation. In construction project management it is applied to verify the accuracy of the forecasts made through Earned Value Management (EVM) methods and assess the sensitivity of schedule activities with Schedule Risk Analysis (SRA).
Benefits of Monte Carlo
All in all, this method can greatly improve decision making by enabling users to see all possible outcomes and account for risk in their quantitative analyses and decision making.
Some other benefits include:

At the same time it should be noted that the cost of running a Monte Carlo simulation can be quite high, despite its conceptual simplicity. As discussed above, for every unknown variable, it randomly draws different values every time, which requires a plethora of samples to get a satisfactory approximation. On the bright side, there are quite a few computing strategies and methods that can significantly reduce this cost … to feasible levels.
Scheduling and Monte Carlo
In the context of construction scheduling, Monte Carlo is used primarily for schedule risk analysis (SRA). In SRA, you connect an existing schedule (baseline) with risk information in order to get sensitivity information and gauge the criticality of tasks, which allows users to assess the potential impact of uncertainty on achieving the project completion date.
In traditional SRA, Monte Carlo is applied to a schedule to check for robustness. In other words, instead of having a single point estimate for an activity duration e.g. 8 hours, the algorithm randomly varies the duration value, produces a set of possible schedules based on those values and reports a set of activity sensitivity measures that score the activity durations in a risk scale. Simply put, it evaluates how likely it is for the activity time estimates to be accurate.
Some activity sensitivity measures that are used are:
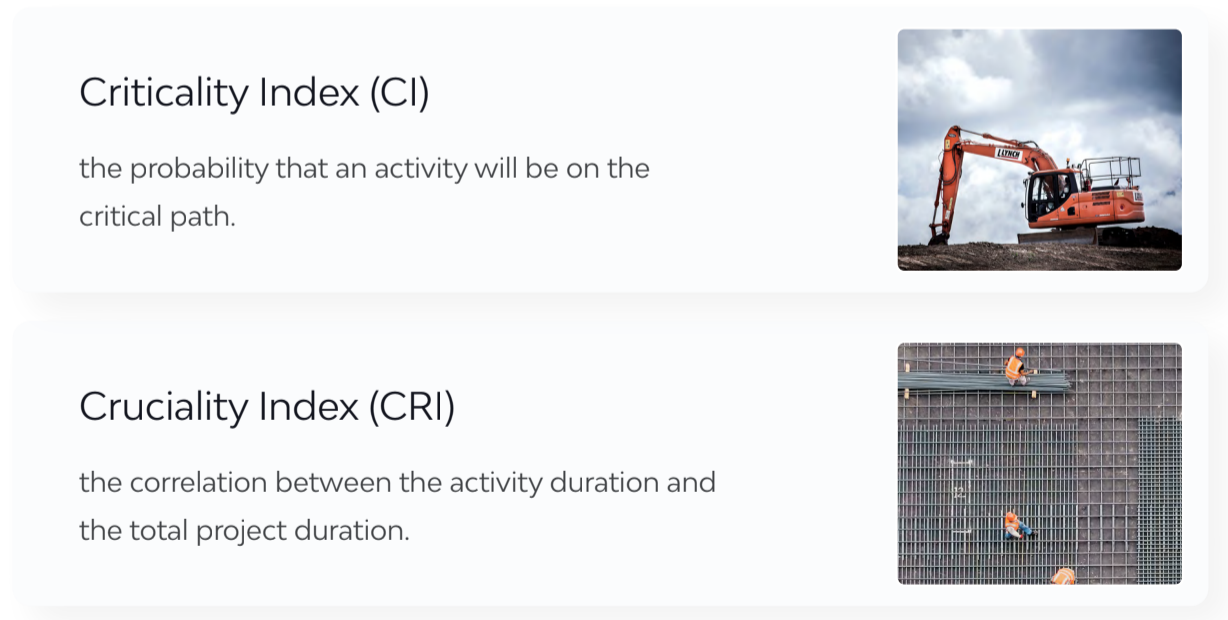
A Project Manager can use these and other sensitivity analysis metrics in order to understand what activities they need to focus on, i.e. which ones are the most risky ones for the project objectives.
ALICE and Monte Carlo
“Does ALICE use Monte Carlo?” is probably one of the most - if not the most - common question we are asked.
In reality, what ALICE does and what Monte Carlo does are two quite different things. ALICE is a modeling engine that generates new optimal solutions (schedules) which satisfy layers of complex constraints. The user defines a problem (simulation model) which the algorithm then solves millions of times to generate the best solution set (see image below). In this way, ALICE provides a deterministic view of outcomes vs a probabilistic view (which is Monte Carlo).
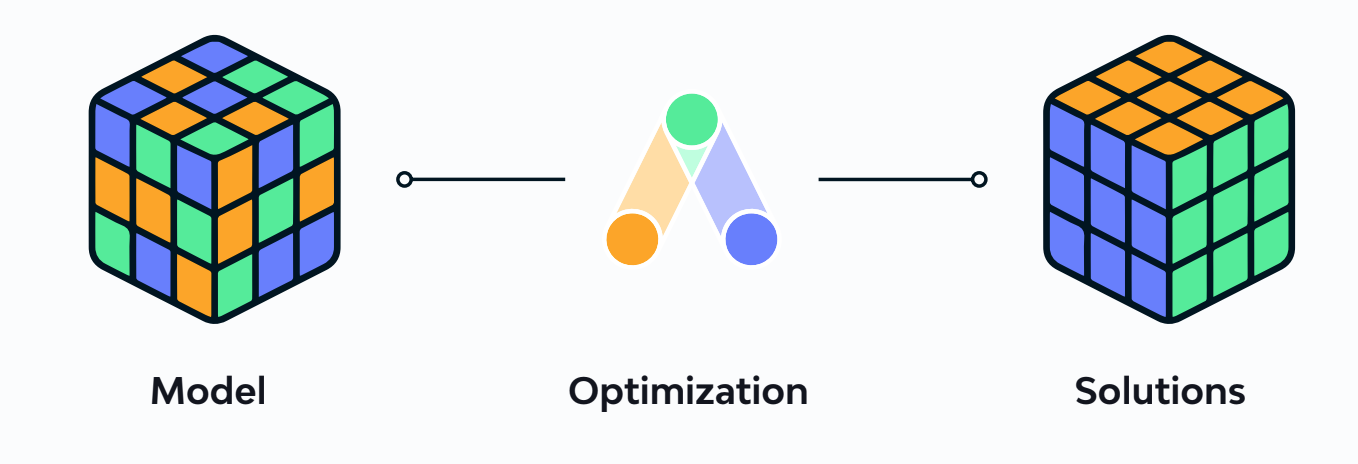
In general, probabilistic methods and metaheuristics have valuable applications to constraint optimization problems. However, in the context of construction scheduling, Monte Carlo traditionally does not resolve constraints to generate solutions. Starting from an existing solution (schedule) a Monte Carlo simulation can be run as a subsequent step to assess how robust the initial solution really is and check the statistical aggregates of the desired risk metrics.
In essence, we have two distinct phases (see image below):
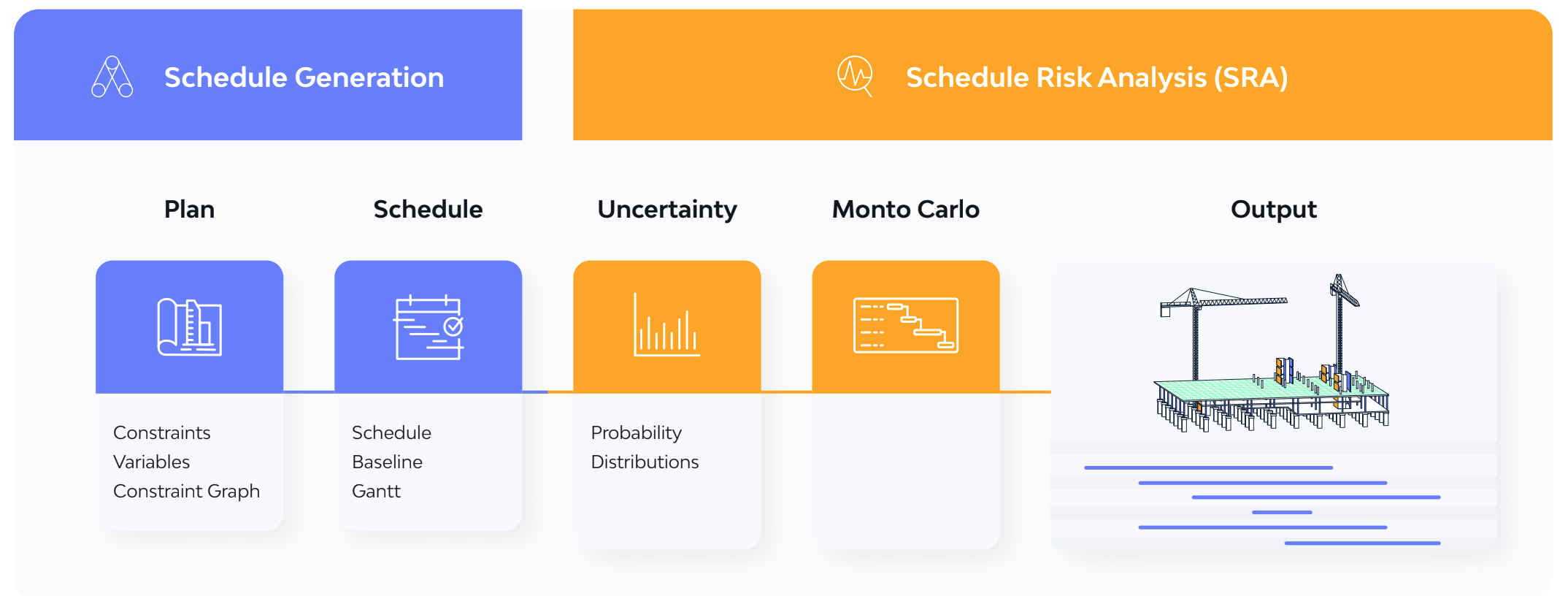
The above schema illustrates how a Monte Carlo simulation can be applied to a schedule generated by ALICE.
The steps can be summarized as follows:

References
-
Kroese, D. P.; Brereton, T.; Taimre, T.; Botev, Z. I. (2014). "Why the Monte Carlo method is so important today". WIREs Comput Stat. 6 (6): 386–392. doi:10.1002/wics.1314. S2CID 18521840.
-
Shonkwiler, R. W.; Mendivil, F. (2009). Explorations in Monte Carlo Methods. Springer.
-
Shojaeefard, MH; Khalkhali, A; Yarmohammadisatri, Sadegh (2017). "An efficient sensitivity analysis method for modified geometry of Macpherson suspension based on Pearson Correlation Coefficient". Vehicle System Dynamics. 55 (6): 827–852.